Introduction¶
This library aims to provide XLA/JAX based Python implementations for various algorithms related to:
Linear operators
Bulk of this library is built using functional programming techniques which is critical for the generation of efficient numerical codes for CPU and GPU architectures.
Sparse approximation and recovery problems¶
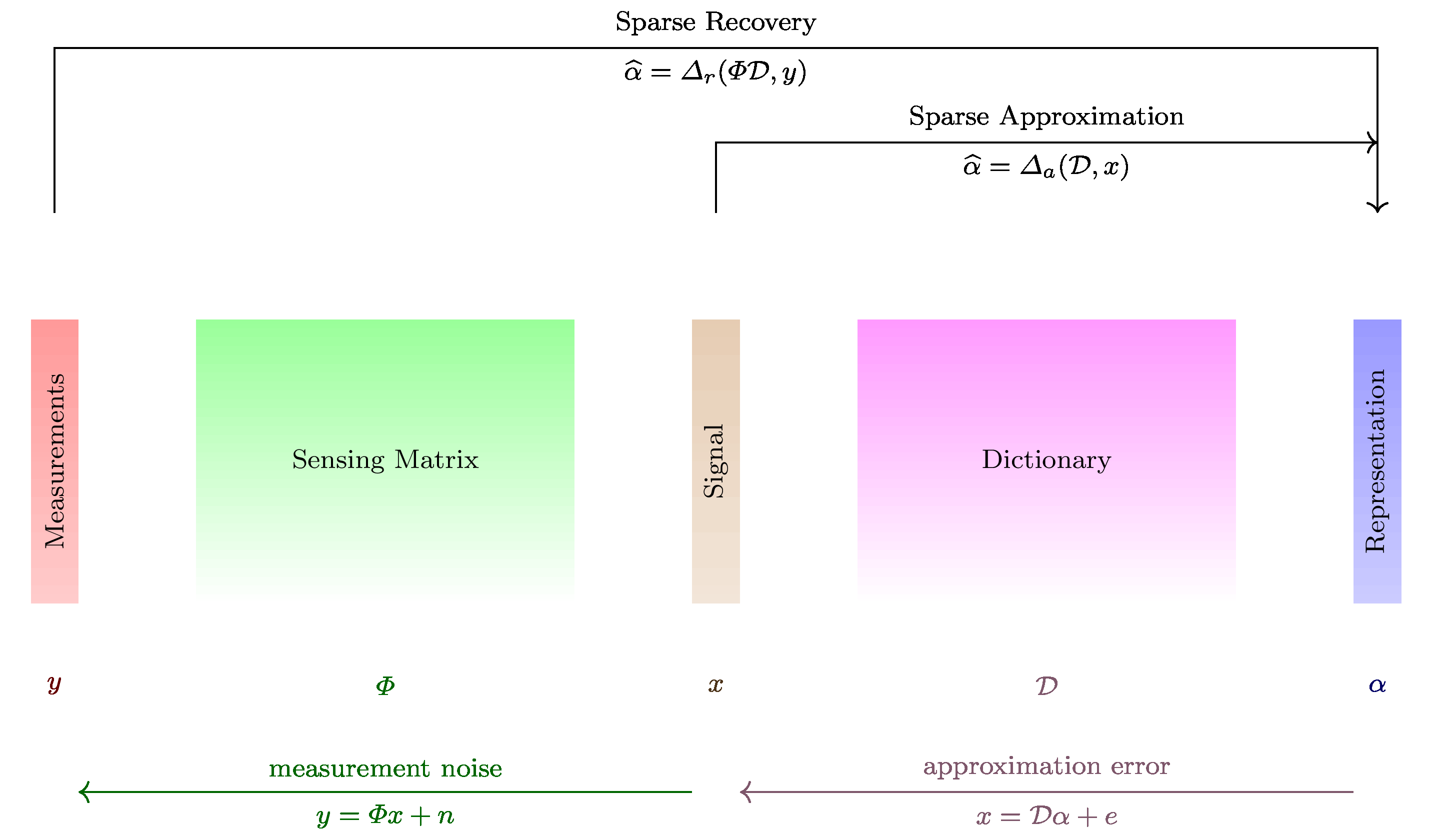
In the sparse approximation problems [Ela10, Mal08], we have a dictionary of atoms designed for a class of signals such that the dictionary enables us to construct a sparse representation of the signal. The sparse and redundant representation model is:
where \(x \in \mathbb{R}^M\) is a single from the given class of signals, \(\mathcal{D} \in \mathbb{R}^{M \times N}\) is a dictionary consisting of \(N\) atoms (column vectors) chosen specifically for the class of signals, \(\alpha\) is the sparse representation of \(x\) in \(\mathcal{D}\) giving us an approximation \(\hat{x} = \mathcal{D} \alpha\) and \(\eta\) is the approximation error. The dictionary \(\mathcal{D}\) is called the sparsifying dictionary. The sparse approximation problem consists of finding the best sparse \(\alpha\) for a given \(x\).
In the compressed sensing (CS) setting, a sparse signal \(x \in \mathbb{R}^N\) is captured through \(M \ll N\) linear measurements which are sufficient to recover \(x\) from the measurements. The model is given by:
where \(y \in \mathbb{R}^M\) is the vector of \(M\) linear measurements on \(x\), \(\Phi \in \mathbb{R}^{M \times N}\) is the sensing matrix [or measurement matrix] whose rows represent the linear functionals on \(x\), \(x \in \mathbb{R}^N\) is the sparse signal being measured and \(e\) is the measurement noise. Typically, \(x\) by itself is not sparse but it has a sparse representation in a sparsifying basis \(\Psi\) as \(x = \Psi \alpha\). The model then becomes:
Sparse recovery consists of finding \(\alpha\) from \(y\) with minimum number of measurements possible.
Both sparse recovery and sparse approximation problems can be addressed by same algorithms (though their performance analysis is different). To simplify the notation, we will refer to \(\mathcal{D}\) or \(\Phi\) or \(\Phi \Psi\) collectively as \(A\) and attempt to solve the under-determined system \(y = A x + e\) with the prior on the solution that very few entries in \(x\) are non-zero. In general, we assume that \(A\) is full rank, unless otherwise specified.
The indices of non-zero entry of \(x\) form the support of \(x\). Corresponding columns in \(A\) participate in the sparse representation of \(y\). We can call these columns also as the support of \(x\).
Recovering the representation \(x\) involves identifying its support \(\Lambda = \mathop{\mathrm{supp}}(x)\) and identifying the non-zero entries over the support. If the support has been correctly identified, a straight-forward way to get the non-zero entries is to compute the least squares solution \(A_{\Lambda}^{\dag} y\). The \(\ell_0\) norm of \(x\) denoted by \(\| x\|_0\) is the number of non-zero entries in \(x\). A representation \(y = A x\) is sparse if \(\| x\|_0 \ll N\). An algorithm which can obtain such a representation is called a sparse coding algorithm.
\(\ell_0\) problems¶
The \(K\)-SPARSE approximation can be formally expressed as:
If the measurements are noiseless, we are interested in exact recovery. The \(K\)-EXACT-SPARSE approximation can be formally expressed as:
We need to discover both the sparse support for \(x\) and the non-zero values over this support. A greedy algorithm attempts to guess the support incrementally and solves a smaller (typically least squares) subproblem to estimate the nonzero values on this support. It then computes the residual \(r = y - A x\) and analyzes the correlation of \(r\) with the atoms in \(A\), via the vector \(h = A^T r\), to improve its guess for the support and update \(x\) accordingly.
\(\ell_1\) problems¶
We introduce the different \(\ell_1\) minimization problems supported by the
cr.sparse.cvx.admm package.
The \(\ell_0\) problems are not convex. Obtaining a global minimizer is not feasible (NP hard). One way around is to use convex relaxation where a cost function is replaced by its convex version. For \(\| x \|_0\), the closest convex function is \(\| x \|_1\) or \(\ell_1\) norm. With this, the exact-sparse recovery problem becomes
This problem is known as Basis Pursuit (BP) in literature. It can be shown that under appropriate conditions on \(A\), the basis pursuit solution coincides with the exact sparse solution. In general, \(\ell_1\)-norm minimization problems tend to give sparse solutions.
If \(x\) is sparse in an sparsifying basis \(\Psi\) as \(x = \Psi \alpha\) (i.e. \(\alpha\) is sparse rather than \(x\)), then we can adapt the BP formulation as
where \(W = \Psi^T\) and \(A\) is the sensing matrix \(\Phi\).
Finally, in specific problems, different atoms of \(\Psi\) may have different importance. In this case, the \(\ell_1\) norm may be adapted to reflect this importance by a non-negative weight vector \(w\):
This is known as the weighted \(\ell_1\) semi-norm.
This gives us the general form of the basis pursuit problem
Usually, the measurement process introduces noise. Thus, a constraint \(A x = b\) is too strict. We can relax this to allow for presence of noise as \(\| A x - b \|_2 \leq \delta\) where \(\delta\) is an upper bound on the norm of the measurement noise or approximation error. This gives us the Basis Pursuit with Inequality Constraints (BPIC) problem:
The more general form is the L1 minimization problem with L2 constraints:
The constrained BPIC problem can be transformed into an equivalent unconstrained convex problem:
This is known as Basis Pursuit Denoising (BPDN) in literature. The more general form is the L1/L2 minimization:
We also support corresponding non-negative counter-parts. The nonnegative basis pursuit problem:
The nonnegative L1/L2 minimization or basis pursuit denoising problem:
The nonnegative L1 minimization problem with L2 constraints:
Functional Programming¶
Functional Programming is a programming paradigm where computer programs are constructed by applying and composing functions. Functions define a tree of expressions which map values to other values (akin to mathematical functions) rather than a sequence of iterative statements. Some famous languages based on functional programming are Haskell and Common Lisp. A key idea in functional programming is a pure function. A pure function has following properties:
The return values are identical for identical arguments.
The function has no side-effects (no mutation of local static variables, non-local variables, etc.).
XLA is a domain-specific compiler for linear algebra. XLA uses JIT (just-in-time) compilation techniques to analyze the structure of a numerical algorithm written using it. It then specializes the algorithm for actual runtime dimensions and types of parameters involved, fuses multiple operations together and emits efficient native machine code for devices like CPUs, GPUs and custom accelerators (like Google TPUs).
JAX is a front-end for XLA and Autograd
with a NumPy inspired API.
Unlike NumPy, JAX arrays are always immutable. While x[0] = 10 is perfectly fine
in NumPy as arrays are mutable, the equivalent functional code in JAX is
x = x.at[0].set(10).
Linear Operators¶
Efficient linear operator implementations provide much faster computations compared to direct matrix vector multiplication. PyLops [RV19] is a popular collection of linear operators implemented in Python.
A linear operator \(T : X \to Y\) connects a model space \(X\) to a data space \(Y\).
A linear operator satisfies following laws:
and
Thus, for a general linear combination:
We are concerned with linear operators \(T : \mathbb{F}^n \to \mathbb{F}^m\) where \(\mathbb{F}\) is either the field of real numbers or complex numbers. \(X = \mathbb{F}^n\) is the model space and \(Y = \mathbb{F}^m\) is the data space. Such a linear operator can be represented by a two dimensional matrix \(A\). The forward operation is given by:
The corresponding adjoint operation is given by:
We represent a linear operator by a pair of functions times and trans.
The times function implements the forward operation while the trans
function implements the adjoint operation.
An inverse problem consists of computing \(x\) given \(y\) and \(A\).
A framework for building and composing linear operators has been
provided in cr.sparse.lop. Functionality includes:
Basic operators: identity, matrix, diagonal, zero, flipud, sum, pad_zeros, symmetrize, restriction, etc.
Signal processing: fourier_basis_1d, dirac_fourier_basis_1d, etc.
Random dictionaries: gaussian_dict, rademacher_dict, random_onb_dict, random_orthonormal_rows_dict, etc.
Operator calculus: neg, scale, add, subtract, compose, transpose, hermitian, hcat, etc.
Additional utilities
Greedy Sparse Recovery/Approximation Algorithms¶
JAX based implementations for the following algorithms are included.
Convex Optimization based Recovery Algorithms¶
Convex optimization [BV04] based methods provide more reliable solutions to sparse recovery problems although they tend to be computationally more complex. The first method appeared around 1998 as basis pursuit [CDS98].
Alternating directions [BPC+11] based methods provide simple yet efficient iterative solutions for sparse recovery.
[YZ11] describes inexact ADMM based solutions
for a variety of \(\ell_1\) minimization problems. The authors
provide a MATLAB package yall1 [ZYY10].
A port of yall1 (Your algorithms for \(\ell_1\)) has been provided.
It provides alternating directions method of multipliers based solutions for
basis pursuit, basis pursuit denoising, basis pursuit with inequality constraints,
their non-negative counterparts and other variants.
Evaluation Framework¶
The library also provides
Various simple dictionaries and sensing matrices
Sample data generation utilities
Framework for evaluation of sparse recovery algorithms
Open Source Credits¶
Major parts of this library are directly influenced by existing projects. While the implementation in CR-Sparse is fresh (based on JAX), it has been possible thanks to the extensive study of existing implementations. We list here some of the major existing projects which have influenced the implementation in CR-Sparse. Let us know if we missed anything.
JAX The overall project structure is heavily influenced by the conventions followed in JAX. We learned the functional programming techniques as applicable for linear algebra work by reading the source code of JAX.
SciPy JAX doesn’t have all parts of SciPy ported yet. Some parts of SciPy have been adapted and re-written (in functional manner) as per the needs of CR-Sparse. E.g.
cr.sparse.dsp.signals. The [TC98] version of CWT incr.sparse.wt.OpTax This helped in understanding how to use Named Tuples as states for iterative algorithms. This was also useful in conceptualizing the structure for
cr.sparse.lop.PyLops: The
cr.sparse.loplibrary is heavily influenced by it.HTP Original implementation of Hard Thresholding Pursuit in MATLAB.
YALL1: This is the original MATLAB implementation of the ADMM based sparse recovery algorithm.
L1-LS is the original MATLAB implementation of the Truncated Newton Interior Points Method for solving the l1-minimization problem.
Sparsify provides the MATLAB implementations of IHT, NIHT, AIHT algorithms.
Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing book code helped a lot in basic understanding of sparse representations.
Further Reading¶
Documentation | Code | Issues | Discussions | Sparse-Plex
