Grassmannian Frames

A Grassmannian (real) frame \(\Phi\) is an \(m \times n\) matrix (dictionary) with unit norm columns such that the individual columns (atoms) are as far away from each other as possible. In other words, it is a matrix with minimum possible coherence. If \(\bG = \Phi^T \Phi\) then every off diagonal entry of the Gram matrix \(\bG\) has the value:

(1)\[|g_{i j} | = \sqrt{\frac{n - m}{m (n - 1)}}\]

Grassmannian frames are hard to construct. CR-Sparse library includes a method based on alternate projections to construct a Grassmannian frame starting from a random dictionary.

# Configure JAX to work with 64-bit floating point precision.
from jax.config import config
config.update("jax_enable_x64", True)

Let’s import necessary libraries

import jax
import numpy as np
import jax.numpy as jnp
import cr.nimble as crn
import cr.sparse as crs
import cr.sparse.dict as crdict
from matplotlib import pyplot as plt

Frame size

m = 50
n = 100

Minimum possible coherence

min_mu = crdict.minimum_coherence(m, n)
print(f'Minimum coherence {min_mu:.5f}')

Minimum coherence 0.10050

Construction of Grassmannian frame

# Start with a Gaussian random dictionary
init = crdict.gaussian_mtx(crn.KEYS[0], m, n)
# Iteratively bring it close to a Grassmannian frame
frame = crdict.build_grassmannian_frame(init, iterations=50)
# The Gram matrix of the final frame
gram = frame.T @ frame
# Off diagonal elements of the gram matrix
off = np.asarray(crn.off_diagonal_elements(gram))
print(f'min: {np.min(off):.3f}, max: {np.max(off):.3f}, mean: {np.mean(np.abs(off)):.5f}')
# Absolute values of the Gram matrix
plt.imshow(np.abs(gram))

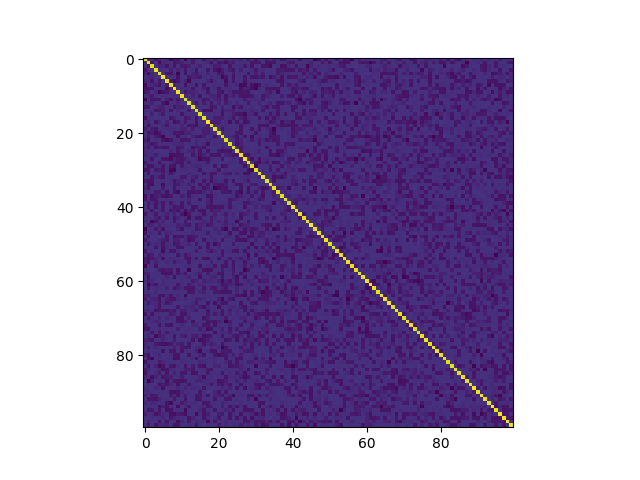
min: -0.160, max: 0.166, mean: 0.11393

<matplotlib.image.AxesImage object at 0x7f27b7701310>