Matching Pursuit

This is a very simple example of using the matching pursuit algorithm.

# Configure JAX to work with 64-bit floating point precision.
from jax.config import config
config.update("jax_enable_x64", True)

Let’s import necessary libraries

# random number generator
from jax import random
# numpy
import numpy as np
import jax.numpy as jnp
# utilities
import cr.nimble as crn
# sample data
import cr.sparse.data as crdata
# linear operators
import cr.sparse.lop as crlop
# matching pursuit algorithm
import cr.sparse.pursuit.mp as mp
import matplotlib.pyplot as plt

Some random number generation keys

key = random.PRNGKey(3)
keys = random.split(key, 5)

Problem setup

# Ambient dimension
n = 400
# Number of non-zero entries in the sparse model
k = 20
# Number of compressive measurements
m = 200

Spikes as sample data

x, omega = crdata.sparse_spikes(keys[0], n, k)
plt.figure(figsize=(8,6), dpi= 100, facecolor='w', edgecolor='k')
plt.plot(x)

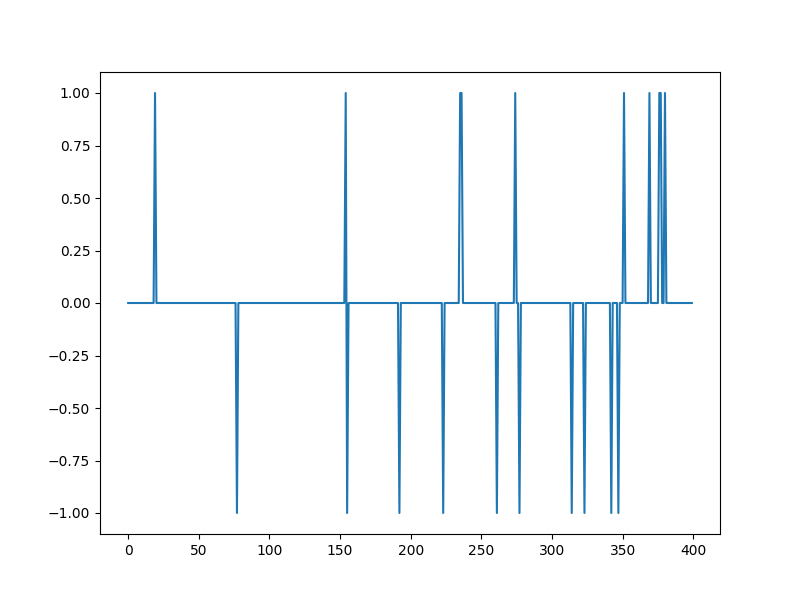
[<matplotlib.lines.Line2D object at 0x7f27abd24730>]

Gaussian sensing matrix linear operator

Phi = crlop.gaussian_dict(keys[1], m, n)
# Make sure that the linear operator is JIT compiled for efficiency.
Phi = crlop.jit(Phi)

Compressive sensing/measurements

Clean measurements

y0 = Phi.times(x)
# Noise
sigma = 0.01
noise = sigma * random.normal(keys[2], (m,))
# Noisy measurements
y = y0 + noise
plt.figure(figsize=(8,6), dpi= 100, facecolor='w', edgecolor='k')
plt.plot(y)
print(f'Measurement noise: {crn.signal_noise_ratio(y0, y):.2f} dB')

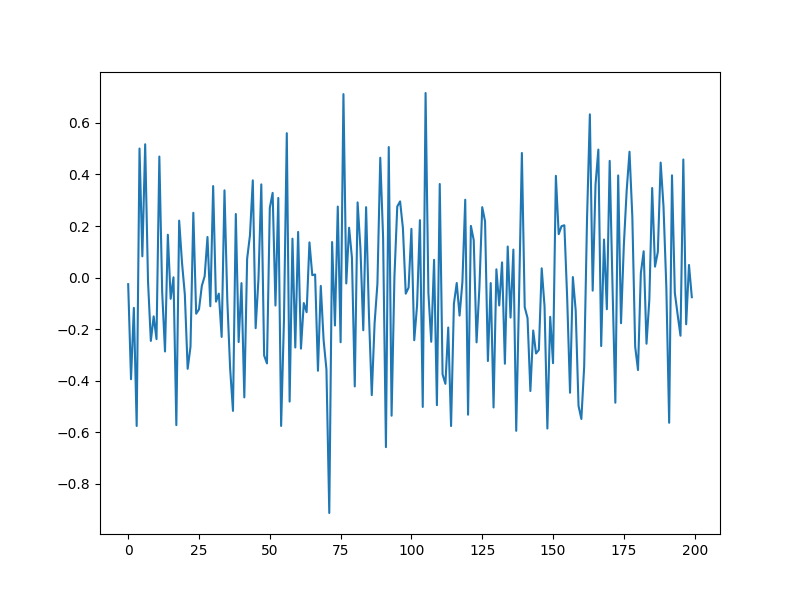
Measurement noise: 30.07 dB

Reconstruction using matching pursuit

sol = mp.solve(Phi, y, max_iters=k*2)
print(sol)
# solution vector
x_hat = sol.x

iterations=40
m=200, n=400, k=22
r_norm=4.318368e+00
x_norm=4.387438e+00

Solution

plt.figure(figsize=(8,6), dpi= 100, facecolor='w', edgecolor='k')
plt.subplot(211)
plt.stem(x)
plt.subplot(212)
plt.stem(x_hat)

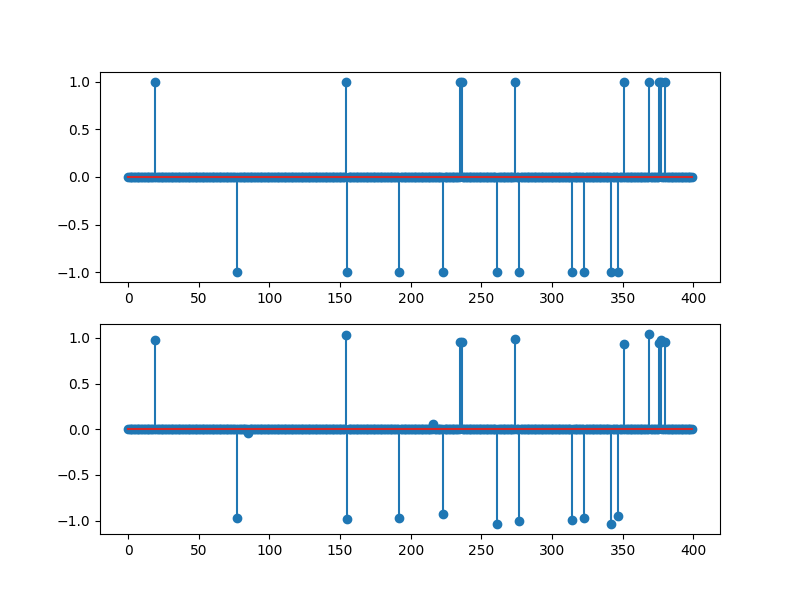
<StemContainer object of 3 artists>

Metrics

snr = crn.signal_noise_ratio(x, x_hat)
prd = crn.percent_rms_diff(x, x_hat)
n_rmse = crn.normalized_root_mse(x, x_hat)
print(f'SNR: {snr:.2f} dB, PRD: {prd:.2f} %, N-RMSE: {n_rmse:.2e}')

SNR: 27.54 dB, PRD: 4.20 %, N-RMSE: 4.20e-02

Verifying the support recovery

print('Support of original signal: ', omega)
print('Support of reconstructed signal: ', sol.I)
# check if every index in the original support is
# also there in the reconstruction support
print(np.all(np.in1d(omega, sol.I)))

Support of original signal:  [ 19  77 154 155 192 223 235 236 261 274 277 314 323 342 347 351 369 376
 377 380]
Support of reconstructed signal:  [ 19  77  85 154 155 192 216 223 235 236 261 274 277 314 323 342 347 351
 369 376 377 380]
True